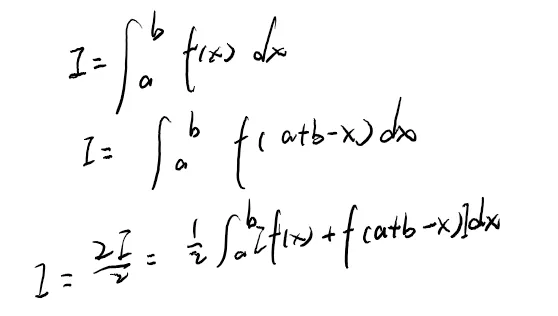📅 时间: 20:59
🌤️ 天气: 银川 23~28℃ 阴
浮云游子意,落日故人情。
— 李白 · 《送友人》
积分公式
- 牛—莱公式: ∫abf(x)dx=F(x)ab=F(b)−F(a)
好用,别忘了fx,FX其实也可以换一种写法f’x,fx
定积分的几何意义:
- 如 ∫0aa2−x2dx=4πa2
- ∫0a2ax−x2dx=4πa2 圆,第二个配下方也一样
奇偶对称性公式:
∫−aaf(x)dx={0,2∫0af(x)dx,if f(x) is oddif f(x) is even
利用奇偶性,这个没啥好说的,为奇的时候挺棒的
- 双非公式: ∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx
拆成(-a,0),(0,a),然后前面那个用t=-x替换,然后因为符号不影响,换回x,就行了
5.轮换对称公式:
∫02πf(sinx)dx=∫02πf(cosx)dxsinx和cosx在 [0,2π] 上的互补关系,画个图像就知道了,定积分求的是面积
6.华里士公式:
In=∫02πsinnxdx=∫02πcosnxdx={nn−1⋅n−2n−3⋯43⋅21⋅2π,nn−1⋅n−2n−3⋯54⋅32,if n is evenif n is odd- 压缩区间公式: ∫0πf(sinx)dx=2∫02πf(sinx)dx sinx 在 [0,π] 区间上的对称性,将积分区间 [0,π] 分成两个部分:[0,2π] 和 [2π,π],u=π−x ∫abf(x)dx=∫a2a+b[f(x)+f(a+b−x)]dx

 本来不好判断正负,区间压缩过后,就可以判断范围正负了 要证明这个积分等式:
本来不好判断正负,区间压缩过后,就可以判断范围正负了 要证明这个积分等式:
∫abf(x)dx=∫a2a+b[f(x)+f(a+b−x)]dx首先,将左侧的积分从 a 到 b 分成两部分:从 a 到 2a+b 和从 2a+b 到 b。
∫abf(x)dx=∫a2a+bf(x)dx+∫2a+bbf(x)dx令 u=a+b−x,则 du=−dx。 当 x=2a+b,u=2a+b;当 x=b,u=a。
∫2a+bbf(x)dx=∫2a+baf(a+b−u)(−du)=∫a2a+bf(a+b−u)du ∫abf(x)dx=∫a2a+bf(x)dx+∫a2a+bf(a+b−u)du注意到第二个积分中的 u 只是一个哑变量,可以将其改回 x:
∫abf(x)dx=∫a2a+bf(x)dx+∫a2a+bf(a+b−x)dx ∫abf(x)dx=∫a2a+b[f(x)+f(a+b−x)]dx证毕
- 消失的X公式: ∫0πxf(sinx)dx=2π∫0πf(sinx)dx
区间再现的特例的一种
- 区间再现公式: ∫abf(x)dx=∫abf(a+b−x)dx=21∫ab[f(x)+f(a+b−x)]dx
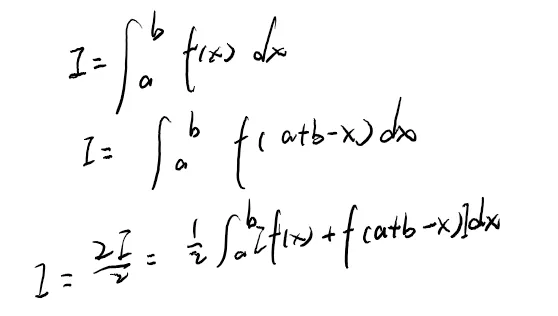
- 周期函数的定积分:
- ∫aa+nTf(x)dx=n∫0Tf(x)dx
- ∫−2T2Tf(x)dx=2∫02Tf(x)dx f(x)为偶函数
- ∫0Tf(x)dx=∫−T/2T/2f(x)dx 对于一个周期为 T 的函数 f(x),它的一个基本性质是:在任意一个长度为 T 的区间上的定积分值都相等

 本来不好判断正负,区间压缩过后,就可以判断范围正负了 要证明这个积分等式:
本来不好判断正负,区间压缩过后,就可以判断范围正负了 要证明这个积分等式: